We'll put the electron on the positive z axis a distance d above the xy plane. Then the only charge in the region z > 0 is the single electron, so we may write the electrostatic potential in that region as the electrostatic potential of the electron plus a term that satisfies the Laplace equation. In the region z < 0 there are no charges, so we may write the potential in that region simply as a term satisfying the Laplace equation. Using the most general azimuthally symmetric solution to the Laplace equation that is regular at the origin, we have
(1) The boundary conditions at the helium surface are
Applying these to Equation (1), we obtain
where
is the relative dielectric constant of liquid helium.Next we multiply the first of these by
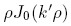and the second by 
, integrate from 
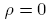to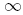 
, and use the identity
to obtain
With help from Mathematica, we find that the first integral equals
, while the second integral equals 
, and we then solve the system to obtain
Then Equation (1) becomes
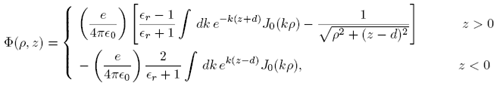
Again using Mathematica to evaluate the integrals, we may simplify this to
We check that the potential in both regions simply reduces to the potential of the point charge when
.To find the electrostatic energy of the point charge, we observe that the first term in the top line of equation (3) represents the potential arising from the surface charge at the helium surface. The electrostatic energy of the electron is just e times this term evaluated at the position of the electron, or
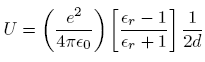
Putting in d = 10 nm and
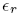= 1.057 for liquid helium at 1 K, we find U 
2.0 meV.