Two lens system – Image distance and magnification

Two converging lenses, with the focal length f₁ = 10 cm and f₂ = 15 cm are placed 40 cm apart, as shown on the figure. An object is placed 60 cm in front of the first lens as show in second figure.
a) Find the position of the final image formed by the combination of the two lenses?
b) Find magnification of the final image formed by the combination of the two lenses?

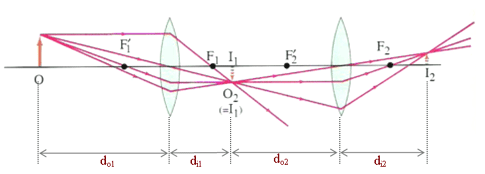L - Distance between two lenses
f₁ - Focal length of first lens
f₂ - Focal length of second lens
d_o1 - Distance to object
d_i1 - Distance to image created from first lens
d_o2 - Distance to object for second lens (which is the image create from first lens)
h_i1 - First image height
h_i2 -Second image height
m₁ - magnification for first lens
m₂ - magnification for second image

To determine the image distance, the lens equation can be used.

Apply lens equation to first lens

d_i1 = 12 cm First image located 12 cm behind the first lens

Image generated from first lens going to be object for the second lens

d_o2 = L – d_i1d_o2 = 40 cm – 12 cm

d_o2 = 28 cm

Lets apply lens equation to second lens

d_i2 = 32.31 cm

Final image located at 32.31 cm behind second lens.

Lens magnification can be find using

m₁ = - 0.2

First lens has magnification of – 0.2
Image magnification in terms of object and image height can be write

First lens has magnification of – 0.2, the image is inverted and is 0.2 times of original height.

Lets apply image magnification equation to second lens

m₂ = - 1.15

Second lens has magnification of – 1.15
Image magnification in terms of object/image height is

Image generated from first lens going to be object for the second lens

h_i1 = h_o2

From this equation we see that total magnification is the product of m₁ and m₂.

Total magnification is 0.23, is a positive number, final image is not inverted but it is smaller than original object.