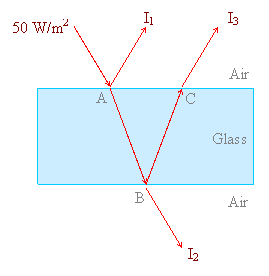
 At point A and B, part of the incident light is transmitted and part is reflected. We defined the reflectance R as the ratio of the intensity of the reflected light Ir to the intensity of incident light Ii. 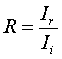 Transmittance is similarly defined as the ratio of transmitted intensity It to incident intensity Ii. 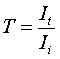 From conservers ion of energy Using above three equations 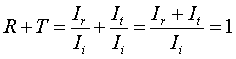 R + T = 1 Equation (4) In the special case of a ray incident normal to the surface, R is found to be a simple function of the indices n and n’. 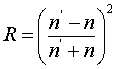 Air to glass 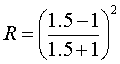 R = 0.04 From equation 4 T = 0.96 Apply equation 1 at point A 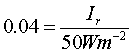 Ir = 2 W/m2 Intensity of the reflected light at point A is 2 W/m2 I1 = 2 W/m2 Using equation 3 It = 48 W/m2 Intensity of the transmitted light at point A is 48 W/m2 Apply equation 2 at point B 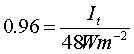 It = 46.08 W/m2 Intensity of the transmitted light at point B is 46.08 W/m2 I2 = 46.08 W/m2 Apply equation 1 at point B 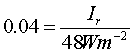 Ir = 1.92 W/m2 Intensity of the reflected light at point B is 1.92 W/m2 Apply equation 2 at point C 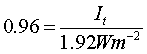 It = 1.84 W/m2 Intensity of the transmitted light at point C is 1.84 W/m2 I3 = 1.84 W/m2 |