Projectile Motion – Pool ball leaves the table with initial horizontal velocity

Home Problems and Answers Classical Mechanics Projectile Motion – Pool ball leaves the table with initial horizontal velocity


A pool ball leaves a 0.20-meter high table with an initial horizontal velocity of 2.4 m/s. Predict the time required for the pool ball to fall to the ground and the horizontal distance between the table's edge and the ball's landing location.

 
Pool ball leaves the table with initial horizontal velocity
 
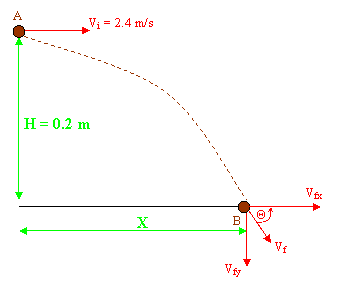
Vi = Initial velocity
Vf = Final velocity
Vx = Horizontal velocity component
Vy = Vertical velocity component
a = Acceleration
t = time
H = Initial height
X = Horizontal displacement
 
For the horizontal motion, the equations are
 
Equations for horizontal motionEquations for horizontal motionEquations for horizontal motion
 
Remember horizontal acceleration is always zero for this problem ( ax = 0). So we can rewrite above equations for horizontal motion as
 
Equation (1)
Equation (1)
Equation (2)
Equation (2)
 
For the vertical motion, the equations are
 
Equations for vertical motion
Equation (3)
For vertical motion - Equations (4)
Equation (4)
 
For vertical motion - Equations (5)
Equation (5)
 
Apply equation (3) for vertical motion from point A to B
 
For vertical motion - Equations (3)
 
At the initial position A, there is no velocity component on vertical direction, so it is zero Vfy = 0
 
For vertical motion
 
For vertical motion
 
Time of flight
 
Time of flight
 
t = 0.2 s
 
Pool ball hit the ground in 0.2 seconds.
 
Apply equation (1) for horizontal motion from point A to B
 
For horizontal motion - Equation (1)
 
Horizontal motion
 
X = 0.48 m
Horizontal displacement 0.48 meters.
 
Lets calculate the final velocity and the angle Θ with horizontal pool ball going to hit the ground. Apply equation (4) for vertical motion from point A to B
 
For vertical motion - Equations (4)
 
Vertical motion
 
Vertical motion
 
Final vertical velocity component
 
Calculate final velocity component.
 
Final velocity on horizontal directions can be easily obtained from equation (2)
 
Velocity on horizontal direction is always equal in this problem
 
Final horizontal velocity component
 
Now we can find the final velocity using trigonometry
 
find the final velocity using trigonometry
 
using trigonometry
 
Final velocity
 
Final velocity
 
Final velocity of the pool ball when it hit the ground is 3.098 m/s
 
Calculate impact angle
 
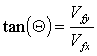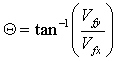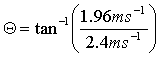incident angle
 
incident angle
 
incident angle
 
incident angle
 
 
Θ = 39.24
 
Angle of incident 39.24 degrees.