Equation of motion for a rocket

Rockets are propelled by the momentum reaction of the exhaust gases expelled from the tail. Since these gases arise from the raction of the fuels carried in the rocket, the mass of the rocket is not constant, but decreases as the fuel is expended.
Show that the equation of motion for a rocket projected vertically upward in a uniform gravitational field, neglecting atmospheric friction, is:

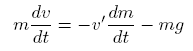
where m is the mass of the rocket and v’ is the velocity of the escaping gases relative to the rocket. Integrate this equation to obtain v as a function of m, assuming a constant time rate of loss of mass.
Show, for a rocket starting initally from rest, with v’ equal to 2.1 km/s and a mass loss per second equal to 1/60th of the intial mass, that in order to reach the escape velocity the ratio of the wight of the fuel to the weight of the empty rocket must be almost 300!
(Source: Herbert Goldstein, Classical Mechanics - Chapter 01)

This problem can be tricky if you are not very careful with the notation. But here is the best way to do it. Defining me equal to the empty rocket mass, m_f is the total fuel mass, m₀ is the intitial rocket mass, that is, m_e + m_f , and

as the loss rate of mass, and finally the goal is to find the ratio of m_f/m_e to be about 300.

The total force is just ma, as in Newton’s second law. The total force on the rocket will be equal to the force due to the gas escaping minus the weight of the rocket:

The rate of lost mass is negative. The velocity is in the negative direction, so, with the two negative signs the term becomes positive.
Use this:

Solve:

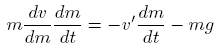
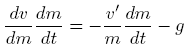
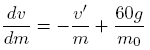
Notice that the two negative signs cancelled out to give us a positive far right term.

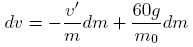
Integrating,

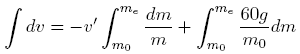
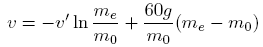
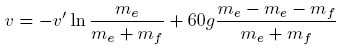
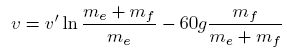
Now watch this, I'm going to use my magic wand of approximation. This is when I say that because I know that the ratio is so big, I can ignore the empty rocket mass as compared to the fuel mass. me << mf

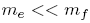. We are looking for this ratio as well. The ratio of the fuel mass to empty rocket, m_f/m_e.

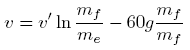
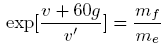
Plug in 11,200 m/s for v, 9.8 for g, and 2100 m/s for v’.

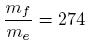
And, by the way, if Goldstein hadn’t just converted 6800 ft/s from his second edition to 2.1 km/s in his third edition without checking his answer, he would have noticed that 2.07 km/s which is a more accurate approximation, yields a ratio of 296. This is more like the number 300 he was looking for.