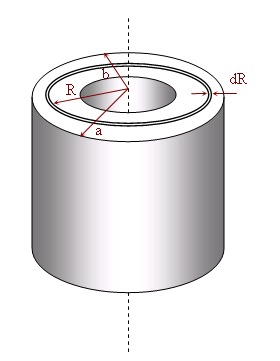
We know that the moment of inertia for hoop with radius R is mR2. We can divide cylinder into thin concentric hoops of thickness dR.
Density = Mass per unit volume
Density = dm / dV
where:Lets assume height of the cylinder is h.
þ; - Density
dm - Mass of a ring or radius R
dV - Volume of a ring or radius R
we have
We can obtain moment of inertia by integrating over all these hoops
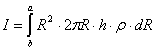
Cylinder has uniform density, where þ = constant
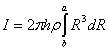
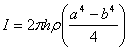
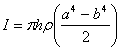
Volume of this cylinder is
Mass M is
since
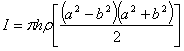
Moment of inertia for hollow cylinder is