E – Energy
p – Momentum
m0 – initial mass
c – Speed of light
The speed of light in a vacuum is exactly 299,792,458 meters per second (or 1,079,252,848.8 km•h-1, which is approximately 186,282.397 miles per second, or 670,616,629.4 miles per hour; sometimes roughly 300,000 km per second)
where γ (the Lorentz factor) is given by
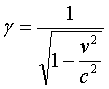
For velocities much smaller than those of light, γ can be approximated using a Taylor series expansion and one finds that
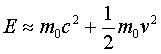
Looking at the above formulas for energy, one sees that when an object is at rest (v = 0 and γ = 1) there is a non-zero energy remaining:
Einstein relationship for energy
Einstein's relativistic mass-energy relation
Relativistic mass
On special relativity sometimes define a relativistic mass which increases as the velocity of a body increases.
Using the relativistic mass definition, the mass of an object may vary depending on the observer's inertial frame in the same way that other properties such as its length may do so.
For example, consider a body with an invariant mass m0 moving at some velocity relative to an observer's reference system. That observer defines the relativistic mass of that body as: