Points of mass joined by rigid rod

Two points of mass m are joined by a rigid weightless rod of length l, the center of which is constrained to move on a circle of radius a. Express the kinetic energy in generalized coordinates.
(Source: Herbert Goldstein, Classical Mechanics - Chapter 01)

Kinetic Energy:

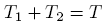
Where T₁ equals the kinetic energy of the center of mass, and T₂ is the kinetic energy about the center of mass. Keep these two parts seperate!

Solve for T₁ first, its the easiest:
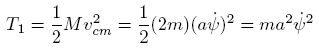
Solve for T1

Solve for T₂, realizing that the rigid rod is not restricted to just the X-Y plane. Don't forget the Z-axis!
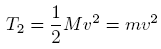
Solve for T2

Solve for v² about the center of mass. The angle

will be the angle in the x-y plane, while the angle

will be the angle from the z-axis.

If

and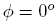

then x = l/2 so:

and

then y = l/2 so:

= 0, then z = l/2 so:

Find v²:

Square each:

Now add, striking out the middle terms:

Pull the first and third terms inside the brackets together, and pull the second and fourth terms together as well:

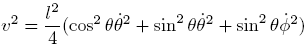
Now that we finally have v² we can plug this into T₂

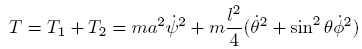
It was important to emphasize that T₁ is the kinetic energy of the total mass around the center of the circle while T₂ is the kinetic energy of the masses about the center of mass.