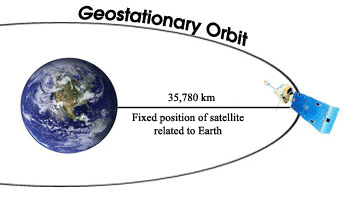
A geostationary orbit is a circular orbit directly above the Earth's equator approximately 35,786 km above ground. Any point on the equator plane revolves about the Earth in the same direction and with the same period as the Earth's rotation.
The period of the satellite is one day or approximately 24 hours. To find the speed of the satellite in orbit we use Newton’s law of gravity and his second law of motion along with that we know about centripetal acceleration. The inward and outward forces on the satellite must equal each another (by Newton's first law of motion).
Fcentripetal = Fcentrifugal
By Newton's second law of motion:
F = ma
where:
ms – Mass of satellite
ag – Gravitational acceleration
ac – Centrifugal acceleration
The centripetal acceleration provided by Earth's gravity:
where:
Me - Mass of Earth in kilograms (5.9742 x1024 kg)
G - Gravitational constant (6.6742 x 10-11 N m2 kg-2 = 6.6742 x 10-11 m3 s-2 kg-1)
Magnitudes of the centrifugal acceleration derived from orbital motion:
where;
ω - Angular velocity in radians per second.
r - Orbital radius in meters as measured from the Earth's centre of mass.
From the relationship
Fcentripetal = Fcentrifugal
We note that the mass of the satellite, ms, appears on both sides, geostationary orbit is independent of the mass of the satellite.
r (Orbital radius) = Earth's equatorial radius + Height of the satellite above the Earth surface
r = 6,378 km + 35,780 km
r = 42,158 km
r = 4.2158 x 107 m
Speed of the satellite is 3.0754 x 103 m/s